SAVE THE DATE FOR NWLDW 2024!
/We are excited to host the New World Luminescence Dating Workshop (NWLDW) June 11-14, 2024 at the Desert Research Institute (DRI) in Reno, NV! Click here for details and updates.
LED2023
/Had an amazing time at LED2023 in Copenhagen last month. Luminescence, ESR dating, a rock surface dating workshop, and a little bit of Viking history! :D
Constraining lateral bedrock erosion rates of the Buffalo National River, Arkansas
/How are wide bedrock river valleys created? How does climate, hydrology, vegetation and tectonism influence the rate of valley widening? To understand this, we need to measure the rate of erosion of bedrock channel walls.
Clay Robertson, PhD candidate at Kansas State University, is researching the influence of talus piles on the evolution of wide bedrock valleys. Talus piles can protect the valley wall from lateral erosion, thus slowing the rate at which valley widening takes place. He is using both sediment and rock surface OSL dating to estimate the residence time for talus blocks sitting along the valley walls of both wide and narrow valleys in the Buffalo National River in northwest Arkansas. In this study, he aims to better constrain the rates at which valleys widen and shed light on the processes required to create wide bedrock valleys, a common geographic feature whose genesis is not yet understood.
Because you are DYING to know...
/We know you are DYING to know how far light can penetrate sandstone rocks in the Buffalo River, Arkansas. So we did an experiment. The answer is…. duh duh duh DUHHHH…. about 10 mm. There you have it. Now you can enjoy the rest of your weekend in peace.
Rock surface dating procedures require that we demonstrate that rock surfaces were adequately sun-exposed prior to burial - incomplete bleaching can lead to residual luminescence signals that give us those pesky age over-estimates. So far, it looks like Buffalo River sandstone bleaches quite well. This should make it easy for us to see similar luminescence signal plateaus in ancient rocks linked to the time of their burial.
Dating limestone
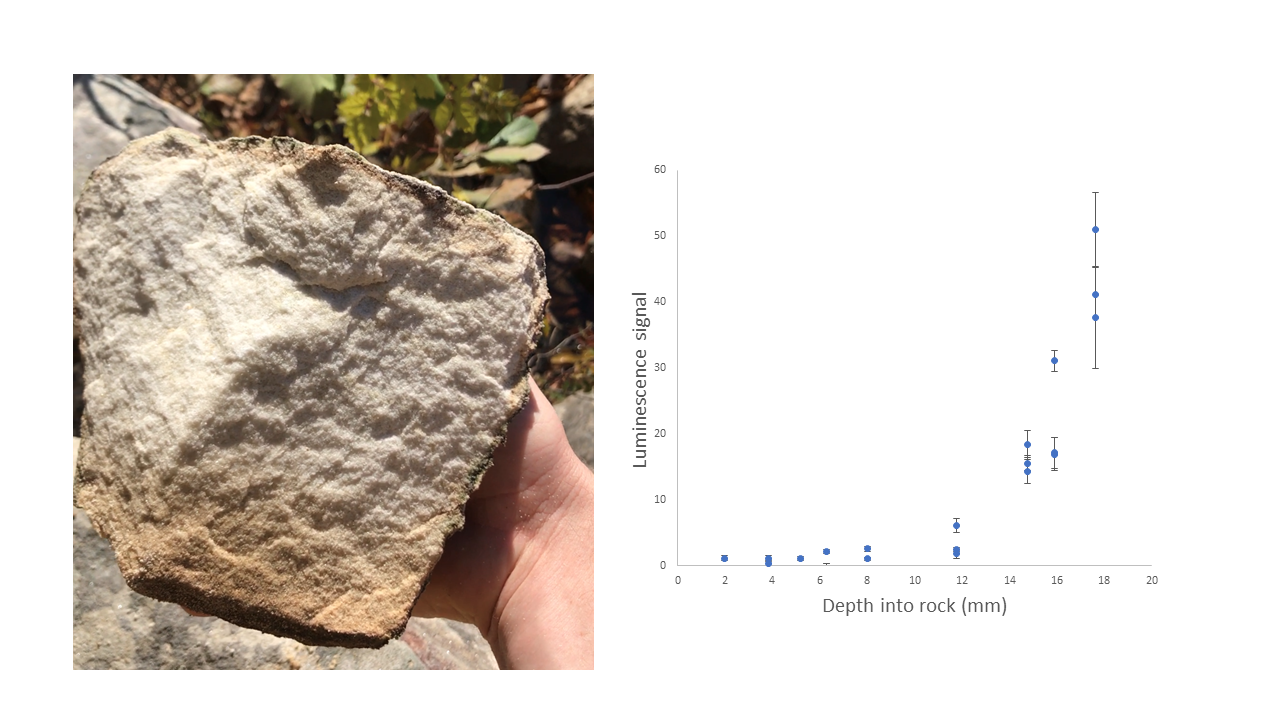
/We know we can OSL date sand and pottery, but how about limestone rocks?? Well, new experimental results at DRILL say YES….. yes we can!
Setting up our new toy!!
/Kathleen Rodrigues setting up our new Lexyg!
Sampling ancient beach ridges in the Great Basin
/No natural exposures here, so we’re diggin’ down from the top! In 110°F, we opted to sample at night using a bottomless tent and tarp to shelter us from the moonlight. (No rattlesnakes or scorpions were harmed during the digging of this pit. ;) )
AGeS2 Program - Awards for Geochronology Student Research2
/The AGeS2 Program is now accepting applications! DRI Luminescence Lab is a participating institution, so if your project could use some “illuminating” geochronology, contact us!
Investigating rates and mechanisms of lateral erosion in a small bedrock river using erosion pins, structure-from-motion photogrammetry, and luminescence dating
/
Abbey Leigh Marcotte has been studying the past and present erosion rates at Kings Creek, an incised stream in northeast Kansas, U.S.A. This system consists of horizontally bedded alternating layers of limestone and shale, presenting a unique setting to study controls on lateral bedrock erosion. Erosion pins and structure from motion were used to determine annual lateral erosion rates and spatio-temporal patterns of erosion along bedrock channel banks. Single-grain optically stimulated luminescence (OSL) dating of fluvial deposits overlying a strath terrace (conducted here at DRILL) was used to determine deposition rates and duration of lateral channel mobility during terrace occupation.
Congrats to Abbey for successfully completing her MSc thesis, and for her new PhD position with the Soil Geography and Landscape Group at Wageningen University, the Netherlands!
A glimpse of pluvial Lake Lahontan in the high desert
/We’re sneaking out of the dark lab for some fresh air and fresh exposures! In the parched high desert of the Carson Sink, Nevada, remnant beach gravels, ridges, loop barriers, tombolos and wave-cut benches record a much wetter past.
(TOP) Beach gravels below and above a well-developed paleosol. The paleosol suggests that the underlying gravels were likely deposited during a lake cycle that predates the most recent (Sehoo) cycle, which reached its maximum ~13,000 years ago. Ken Adams, Research Professor, DRI shown on the right. (BOTTOM) Interference ripples that formed in fine grain sediments on the lake floor.
A radiocarbon age of 13,070 +/- 60 years from camel bones found above beach barrier gravels and below lagoonal sands provides a precise age estimate for the most recent (Sehoo) highstand of Lake Lahontan. This week, we’re digging some more trenches to find out when the lake reached its highstand during earlier (e.g., Eetza) lake cycles over 120,000 years ago.
Jessup Embayment, Carson Sink, Nevada.
Brad Sion, Assistant Research Professor, DRI, ruminating over Sehoo highstand beach gravels exposed in a beach ridge.
Platy, angular volcanic shards forming a desert pavement atop a Sehoo highstand beach ridge.
Tephra in the Lahontan basin - a reliable chronostratigraphic marker?
/Congrats to our new Postdoc, Kathleen Rodrigues, who was recently awarded an NSF grant to investigate the time of final deposition of tephras in the Lahontan basin!
Tephras, which are products of volcanic eruptions, are significant markers in the stratigraphic record and have an important role in establishing paleoenvironmental and paleoclimate histories worldwide. The use of tephras (or any stratigraphic markers) in the documentation of Earth’s history involves fundamental assumptions about the unit including: deposition at a single point in geologic time, no reworking since deposition, and that the age of the unit can be definitively determined, preferably with multiple independent geochronologic tools. Because volcanic eruptions typically occur over short geologic time scales, the deposits associated with them are considered to represent a single short-lived event. However, reworking of tephras may take place over longer timescales complicating stratigraphic correlation among outcrops (Lowe and Alloway, 2014).
The objectives of this research is to i) quantify the timescales over which tephra reworking occurs using routine luminescence dating techniques, ii) test recently developed luminescence dating techniques designed to directly date tephras in the 35-120 ka age range, and iii) combine the results of objectives 1 and 2 to unravel the late Pleistocene and Holocene history of pluvial lake expansion and contraction in the Lake Lahontan basin.
Congrats Kathleen!
/Congrats to Kathleen Rodrigues for successfully defending her PhD thesis on the “Development and application of luminescence dating techniques to constrain the timing of tephra deposition and the formation of fluvial landforms”!
Abstract
Interest in earth surface processes has grown substantially in recent years owing, in part, to improvements to scientific methodology and a greater awareness of the impacts that humans and climate have on the on the earth’s surface. The geological record contains sedimentary archives that can be used to interpret the sensitivity of a variety of environments to anthropogenic and/or natural forcings. However, developing these interpretations over long time scales fundamentally requires accurate geochronology to place absolute ages on individual geological events. Luminescence dating, a geochronological technique used for estimating the last exposure of a material to light or heat, has emerged as a promising method for dating Quaternary events and constraining the timing of environmental changes. In addition to a review of the physical processes involved in luminescence geochronology, the work described in this PhD dissertation has broadly centered on two luminescence-based research endeavors: (1) the development of novel thermoluminescence (TL) techniques for dating volcanic glasses, and (2) the application of optically stimulated luminescence (OSL) dating techniques to strath terraces.
In Part 1, we test different TL dating approaches on the 4-11 μm volcanic glass constituents of three different tephras. By comparing against independent age control, we demonstrate the utility of both blue (320 nm to 450 nm) and red (587 nm to 651 nm) TL emissions for dating volcanic glasses using single aliquot regenerative dose techniques (SAR). We find that both blue and red TL emissions from the volcanic glass shards are dim but reproducible and show no evidence for significant sensitivity changes occurring between the natural TL and the first test dose during the SAR protocol. Fading tests on the blue TL signal show that g-values range from 1.23 ± 1.10 to 3.13 ± 1.29 %/decade and are statistically consistent with zero at 2σ for the red TL. Bleaching experiments show that both signals are sensitive to light exposure, with sensitivity corrected signals declining by ~60% and ~40% over a 2-hour period for blue and red TL signals, respectively. With the exception of one sample, the Turupah Flat tephra, which yields both blue and red TL ages ~600 years older than local independent age control, both the fading-corrected blue and red SAR-TL ages are fully consistent with age expectation. These successful results demonstrate the effectiveness of TL techniques for determining the eruption ages of tephra deposits in primary position between ~1.5 and 30 ka. Blue and red TL dose response behavior suggest that average characteristic saturation doses are ~1200 Gy, which corresponds to an upper dating limit of ~400 ka in dose rate environments similar to the ones we observed.
In Part 2, we apply quartz OSL dating techniques to alluvium overlying strath terraces along the Buffalo National River (BNR) where incision has occurred across lithologies of variable resistance during the Quaternary. OSL-derived incision rates ranged from 0.3 mm/yr in the more resistant sandstone-dominated reaches relative to 0.03 mm/yr in the less resistant limestone-dominated reaches. Comparisons of these incision rates with estimates of lateral migration based on in-situ produced 10Be concentrations support the hypothesis that lateral processes outpace vertical ones in the less resistant reaches of the BNR. These results suggest that lithologic resistance imparts a strong influence on both the rates and styles of incision and consequently on landscape evolution. Importantly, our OSL results also demonstrate that overbank deposition can occur thousands of years after strath terrace abandonment even 5+ m above the modern channel, and that chronologies developed from sampling alluvial drapes can be subject to erroneous age interpretation.
Together, these works encompass a body of research covering a breadth of topics in luminescence dating from fundamental principles, to technique development and application. The outcomes of this work not only contribute to a broader understanding of the luminescence process, but also the development and improvement of methods and sampling strategies for quantitative reconstruction of the geologic record over the Quaternary.
Dating Dry Valley Deltas Down Under
/
Michael Stone, PhD student at Louisiana State University, is interested in understanding how Lake Fryxell, and its surrounding ecosystem responded to climate fluctuations in the McMurdo Dry Valleys, Antarctica. By dating perched deltas, he’s reconstructing the history of lake level change, which in turn can tell us more about the timing of the retreat of the Ross Ice Sheet following the last glaciation. At DRILL, Michael is dating perched deltas using single grains of feldspar. The age distribution derived from multiple grains from each sample not only gives us an age estimate for the delta, but also tells us about the bleaching history of the grains, and therefore the delta surface conditions at the time of sediment deposition.
The science of light and lithology
/The ages of rock surfaces can help us determine the timing of past lake or sea level change (e.g., Simkins et al., 2013), the advance and retreat of glaciers (Jenkins et al., 2018), and the construction of monuments, buildings or walls by ancient humans (Liritzis, 2010), to name a few. Luminescence ages from rocks are important for sites that lack adequate sediment for traditional luminescence dating techniques, as well as sites that are contaminated by mobile fine grain materials that severely post-date (underestimate) the true age of the landform or artifact.
But here in the Great Basin, which rocks are the brightest?
We’ve sampled a range of rock types from various locations in Nevada to see which lithologies have luminescence signals suitable for dating.
Preliminary results suggest that most sedimentary and felsic volcanic rocks have a detectable signal from feldspar, some sedimentary rocks have detectable signal from quartz, and basalt, sinter, and hydrothermal quartz have very dim or no signals at all. At DRILL, we are conducting experiments to further characterize the signals from Nevadan rocks so that new dating techniques can be developed.
OSL, IRSL, and post-IR OSL signals from a range of rock types from Nevada. Click here for more information on luminescence signal types and how they are used.
Luminescence dating ancient pluvial lake shorelines in the Lake Lahontan basin using.... tufa?
/Well, we know we can determine the age of sand using luminescence dating here at DRILL. But can we date tufa?? We’re gonna try! Many ancient shorelines in the Lahontan basin are cemented in carbonates (tufa) that precipitated out of lacustrine waters.
The Jessup embayment preserves shoreline features mainly dating to the last (Sehoo) lake cycle in the Late Pleistocene. The sampled lithoid terrace at 1339 m asl, with tufa coated beach cobbles, may have started to form during the penultimate (Eetza) lake cycle ~100,000 years earlier (Adams & Wesnousky 1998; 1999).
As it turns out, these carbonates contain silt and sand that would have been exposed to sunlight in the nearshore environment, making them interesting candidates for luminescence dating. We’ve sampled tufa from a cobble beach deposit associated with a former pluvial lake highstand in the Jessup embayment to determine its potential for dating.
TOP. The sampled lithoid terrace in the Jessup embayment. Person for scale. BOTTOM LEFT. Lithoid tufa. BOTTOM CENTER. The IRSL signal from silt (<32 um) extracted from the tufa. BOTTOM RIGHT. A fading plot showing a moderate to high fading rate.
Results so far show that i) up to ~13% of this tufa consists of sediment, ii) this sediment has a sufficiently bright IRSL signal for dating, and iii) the IRSL signal has a moderate to high fading rate. Future work will explore the potential of other luminescence signals that will depend less heavily on fading corrections.
Wishing you health and resilience
/Thanks to the IT team at DRI for providing us with remote access to our desktop computers during COVID-19! We wish the best of health and resilience to all friends and colleagues in these trying times.
Rock surface dating using luminescence methods
/
Luminescence dating techniques are most commonly applied to sand or silt sediments, but methods have been developed in recent decades that also allow us to date rock surfaces (e.g., Freiesleben et al. 2015; Gilganic et al. 2019). DRILL is currently experimenting with rock surface dating techniques using luminescence. Thanks so much to James Feathers at University of Washington for letting us use his precision saw and rock coring equipment. The Luminescence Dating Lab in the Department of Anthropology at UW has been in operation in since 1993, and it was a great opportunity to pick the brain of a scientist with decades of experience in the field.
A Buehler precision saw with a 400 µm thick diamond wafer blade allows us to cut rock cores into sub-millimeter thick slices. These can be used to date the last time a rock surface has been exposed to sunlight, and to determine the depth of light penetration in a rock.
Luminescence signals - a cheat sheet
/
Despite the fact that the vast majority of samples we date here at DRILL are dated using optically stimulated luminescence (OSL) techniques, some colleagues still refer to our lab as “the TL lab”. This is because thermoluminescence (TL) dating techniques, still used today, are the precursors to “optically stimulated luminescence” dating techniques developed more recently in the 1980’s. TL measures the luminescence of a sample emitted when it is exposed to heat, and OSL measures the luminescence of a sample when it is exposed to light. Both methods can determine the last time a sample has been exposed to light or heat, however OSL is now typically used to determine a burial age – the time since the sample was exposed to the sun.
But it does not end there….
In recent decades, a myriad of luminescence signals with distinct characteristics have been explored. Which signal is most applicable to your project depends on the expected age of the sample, the mineral(s) to be dated, the event to be dated (i.e. last light/heat exposure), the optical properties of the minerals, as well as their depositional history. Here we provide a cheat-sheet for luminescence signal jargon commonly seen in the literature. This list is always growing, so don’t hesitate to let us know if we’re missing one!
The New World Luminescence Portable Gamma Spectrometer Calibration Initiative!
/On the weekend of October 19th, 2019 luminescence specialists representing seven North American research institutions met at the Calibration Facility at Grand Junction Airport, Colorado to calibrate their portable gamma spectrometers and perform inter-lab comparisons of their measurements. This meeting was the first of a series that will occur annually to ensure portable gamma spectrometers are calibrated to standard.
Portable gamma spectrometers can be used in the field to measure the gamma radiation of sediments/rocks from which luminescence samples have been collected. These in situ measurements are considered especially important at sites where the gamma radiation dose field is heterogeneous. Heterogeneities in the gamma dose field will occur if sampled sediments are variable in their granulometry, organic matter/water content, and/or are proximal to sedimentary units of different composition.
This year’s participants included: Shannon Mahan (USGS), Tammy Rittenour & Michelle Nelson (Utah State University), Christopher Garcia (East Carolina University), Sebastien Huot (Illinois Geological Survey), Christina Neudorf (Desert Research Institute & University of the Fraser Valley) and David Sammeth (New Mexico Highlands University).
